A-level 物理/宇宙学/已知宇宙模型

随着更先进的工具的开发，我们对宇宙的理解也得到了改善。一些提出的宇宙模型被证明是错误的，而其他想法至今仍存在。

测量宇宙中的距离

宇宙尺度的距离是巨大的，我们日常使用的米甚至公里都太小了。我们需要使用更适合大距离的单位。通常，其他单位使用起来很方便，因为它们是通过测量得到的。

光年

一光年定义为光在一年内传播的距离。如你所知，光速为 $3\times 10^{8}$ ${\text{ms}}^{-1}$，因此它在一年的时间内传播的距离非常巨大。一光年大约为 $10^{16}{\text{m}}$.

天文单位

天文单位定义为地球和太阳之间的平均距离。它起源于这样一个事实：可以测量行星的距离，但只能以地球和太阳之间的距离为倍数。它在今天仍然适用于太阳系内的距离。它大约等于 $1.5\times 10^{11}{\text{m}}$.

视差的简化示例。

秒差距

一秒差距仅仅是恒星从地球轨道上的两个对立点观察时视差角的一半的倒数。视差是指当观察者位置改变时，物体相对于固定背景的视位置的变化，就像你在汽车里时，建筑物看起来比背景山丘移动得更快一样。它从测量的角度方便地求出，因此主要用于恒星的距离。这个概念将在 恒星和星系 中详细介绍。一秒差距大约为 $3\times 10^{16}{\text{m}}$，或者 3.26 光年。

太阳系的概述

太阳系，显示了太阳、行星、火星和木星之间的小行星带，以及一颗彗星。

我们的太阳系包括太阳、行星和一个小行星带。此外，还有彗星，它们具有高度椭圆的轨道，并定期返回太阳系。

行星

有八颗行星绕太阳运行（冥王星被重新归类为矮行星），太阳位于太阳系的中心。大多数行星也有天然卫星，或称为卫星，绕它们运行。下表概述了行星相对于地球的主要特征。

行星	赤道 直径	质量	轨道 半径 (天文单位)	轨道周期 (年)	轨道 倾斜 角度 (°)	轨道 偏心率	日 (天)	卫星
水星	0.382	0.06	0.387	0.241	7.00	0.206	58.6	无
金星	0.949	0.82	0.72	0.615	3.39	0.0068	-243	无
地球	1.00	1.00	1.00	1.00	0.00	0.0167	1.00	1
火星	0.53	0.11	1.52	1.88	1.85	0.0934	1.03	2
木星	11.2	318	5.20	11.86	1.31	0.0484	0.414	63
土星	9.41	95	9.54	29.46	2.48	0.0542	0.426	49
天王星	3.98	14.6	19.22	84.01	0.77	0.0472	-0.718	27
海王星	3.81	17.2	30.06	164.8	1.77	0.0086	0.671	13
冥王星	0.18	0.002	39.5	248.5	17.1	0.249	-6.4	4

小行星带

火星和木星之间存在着小行星的密集区域，被称为小行星带。有成千上万颗这样的类行星绕太阳运行，有时也被称为小行星。

彗星

彗星是由岩石、冰冻水、甲烷和氨组成的团块，绕太阳运行，通常只有几公里宽。它们拥有非常偏心（椭圆形）的轨道，因此它们与太阳之间的距离变化很大。当它们靠近太阳时，由于太阳辐射，它们会有长达 1 个天文单位的尾巴。

对宇宙的理解进步

太阳系的公认模型在过去几十年中一直备受争议。在旧的地心说模型中，地球最初被置于太阳系的中心，其他行星和太阳围绕它运行。现在，公认的模型将太阳置于中心，地球和其他行星围绕它运行。

哥白尼

火星的逆行运动

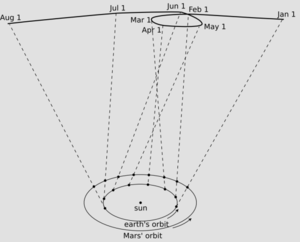
尼古拉·哥白尼发现旧的地心说模型过于复杂。他决定将太阳而不是地球置于宇宙的中心，这就是我们现在所说的日心说模型。这个模型可以很容易地解释行星和太阳在天空中运动的情况，尤其是火星的逆行运动，即火星在天空中的运动方向似乎会在几周内“倒退”。以前人们用本轮来解释这种火星的逆行运动，认为它会在某些点进行“循环运动”。哥白尼的新模型解释说，由于地球比火星离太阳更近，在地球“超越”火星的阶段，火星在天空中的运动方向看起来会“倒退”。

对哥白尼的反对

哥白尼的日心说模型主要因为当时人们的宗教信仰而遭到大多数人的拒绝，尽管它似乎简化了行星的运动，但它在拟合观测到的行星运动方面不如地心说准确。

人们还认为，如果地球在运动，恒星应该会有可检测的视差。哥白尼声称恒星距离太远，无法检测到任何视差，随着更灵敏设备的出现，他现在被证明是正确的。另一个反对日心说的论点是，所有物体都朝地球落下，因此地球一定是宇宙的中心。这在牛顿彻底改变我们对运动的认识之前是人们直观的结论。

开普勒

以太阳为一个焦点的椭圆轨道

约翰内斯·开普勒通过使用椭圆轨道而不是圆形轨道来改进哥白尼的原始模型。他制定了行星运动的三大定律。

开普勒第一定律

开普勒发现，如果行星在椭圆而不是圆形轨道上运动，并且太阳位于这些椭圆的其中一个焦点上，那么行星更符合观测到的模式。因此，开普勒第一定律指出

行星以太阳为一个焦点的椭圆轨道绕太阳运行。

开普勒第二定律

等时间内扫过等面积

现在行星有了椭圆轨道，它们在轨道上的所有点以相同速度运动就没有意义了。行星在靠近太阳时会加速，在远离太阳时会减速。开普勒观察到，如果行星轨道的两个点之间的时差相同，则由行星在两个点上的位置和太阳形成的虚线三角形始终具有相同的面积。由此得出，行星在靠近太阳时比远离太阳时运行得更快。开普勒第二定律指出

连接行星和太阳的直线在等时间内扫过等面积。

椭圆的长半轴

开普勒第三定律

开普勒意识到，行星到太阳的距离与其轨道周期之间存在关系：$T^{2}\propto d^{3}$，其中 T 是绕太阳运行一周所需的时间，d 是到太阳的距离，但实际上是长半轴的长度（即椭圆最长直径的一半）。

轨道周期的平方与到太阳距离的立方成正比。

伽利略

金星的相位。

伽利略·伽利雷是第一个使用望远镜观测夜空的人。他能看到肉眼看不到的许多东西，比如月球表面不完美，以及天空中有许多暗淡的星星。这两点都支持了哥白尼的观点。

伽利略和金星

当伽利略用他的望远镜观察金星时，他注意到金星像月球一样经历相位变化。他还注意到，当金星呈新月状时，它比满月时要大得多。这一观察结果证明了金星绕太阳而不是地球运行。

伽利略和木星的卫星

伽利略还观察到四个天体绕木星运行，这些天体现在被称为伽利略卫星。它们支持了并非所有天体都绕地球运行的观点。

牛顿的万有引力定律

当艾萨克·牛顿创建他的万有引力定律时，他试图证明开普勒对行星运动的观察与他的定律一致。这有力地证明了他是正确的。

牛顿的万有引力定律可以用来给出行星的公式形式$T^{2}\propto d^{3}$

太阳与行星之间的万有引力等于使行星保持在轨道上所需的向心力。

$F=G{\frac {m_{1}m_{2}}{d^{2}}}={\frac {mv^{2}}{d}}$

行星轨道周期的计算公式为

${\text{Time taken}}={\frac {\text{distance}}{\text{velocity}}}$

其中，距离为圆周长，即 $2\pi \times d$ （注意，d 为距离太阳的距离，即半径，不是直径）。 因此，我们有

$T={\frac {2\pi d}{v}}$

我们可以将公式重新整理，使 v 成为主体，并将它代入到向心力公式中的 $v^{2}$

$v={\frac {2\pi d}{T}}$

$v^{2}={\frac {4\pi ^{2}d^{2}}{T^{2}}}$

$G{\frac {m_{1}m_{2}}{d^{2}}}={\frac {4\pi ^{2}md}{T^{2}}}$

消除行星质量 m，并将公式整理

$G{\frac {mT^{2}}{4\pi ^{2}d^{3}}}=1$

最后，将 $T^{2}$ 作为主体

$T^{2}={\frac {4\pi ^{2}}{Gm}}d^{3}$

我们现在得到了一个 $T^{2}\propto d^{3}$ 的形式，比例常数为 ${\frac {4\pi ^{2}}{Gm}}$，其中 m 为太阳的质量。

海王星的发现

1821 年，亚历克西斯·布瓦尔德发表了关于天王星轨道非常准确的观测结果。但是，不久之后，天王星的轨道被发现偏离了发表的数值。 1845 年，约翰·亚当斯利用牛顿的万有引力定律计算了天王星轨道外另一颗行星的轨道，该行星的引力可以解释天王星轨道上的 **扰动**。 海王星在一年后被发现于其预测的位置。 冥王星的发现也是通过类似的方法，因为它导致了天王星和海王星轨道上的进一步扰动。

牛顿理论遇到的问题

尽管牛顿的理论在解释行星运动方面非常成功，甚至被用来发现未知行星，但它仍然存在一些问题。

• 观测发现水星的轨道与该理论预测的轨道不同。现在，爱因斯坦的广义相对论已经解决了这个问题。
• 如果宇宙中每个物体都相互吸引，那么整个宇宙就应该由于引力吸引而坍缩。为了解决这个问题，牛顿提出了一个想法，即宇宙是无限大的，物质均匀地分布在整个宇宙中。然而，这导致了它自己的问题，即奥伯斯佯谬，该佯谬指出，一个无限大的宇宙在任何给定的视线方向上始终会有一个恒星，因此夜空实际上应该很亮。这个矛盾已经被埃德温·哈勃观测到的宇宙膨胀解决了。