A-level 物理/力学、场与能量/万有引力场

我们已经接触过万有引力场，其中行星的万有引力场强乘以物体的质量就等于该物体的重量，地球的万有引力场强 $g$ 等于其表面上的自由落体加速度 $9.81\,\mathrm {ms^{-2}}$。现在我们将考虑不均匀的万有引力场，以及如何计算 $g$ 的值，针对任何给定的质量。

万有引力场

地球的万有引力作用范围延伸到太空中很远的地方。例如，月球受到地球万有引力的影响，即使它距离地球 400,000 公里（在那里万有引力是向心力）。地球有一个万有引力场，会吸引任何有质量的物体朝向地球中心。

径向场

地球的径向万有引力场由这些线表示。

万有引力场是包围地球的一个区域，在这个区域中，另一个物体会感觉到引力。该力的方向朝向地球中心，或者一般来说是朝向质量中心。距离越远的物体感受到的引力越小，而距离越近的物体感受到的引力越大。

均匀场

万有引力场线表示是任意的，如这里所示，在 30x30 网格到 0x0 网格中表示，几乎平行且直指地球中心。

地球的万有引力场由小尺度上的平行线表示。

然而，**均匀场**的线完全平行。地球的万有引力场可以认为在汽车、球和飞机等小物体尺度上是均匀的。在这个尺度上，对于较小的高度（几十公里），场强的变化不足以察觉。同样，箭头指向地球中心，因为物体就是那样下落的。

牛顿的万有引力理论

艾萨克·牛顿试图找到一种方法来解释为什么物体落向地球中心而不是仅仅停留在原地。他开始将苹果下落与月球“落向”地球联系起来，并提出了他的**万有引力定律**。

他认为，任何两个有质量的物体之间都会存在引力。这种引力与它们的质量成正比，因此质量越大的物体之间的引力就越强。

每个物体的万有引力场都是径向场，因为质量集中在物体的中心，如你所知，这就是万有引力可以被认为起作用的地方。

如你所见，当距离加倍时，四分之一的力线穿过该平面。

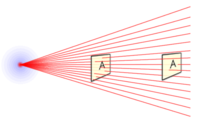
径向场的强度随着你离它越远而减弱。正如你在右边图中看到的，穿过该平面的场线数量在距离加倍时变为四分之一，如果距离增加三倍，它将是原始值的 ${\frac {1}{9}}$。

这被称为平方反比定律，对于任何点源来说都是成立的，比如来自一个点的光或辐射量。

平方反比定律遵循 ${\frac {1}{r^{2}}}$。

利用以上，牛顿认为引力与两个质量以及它们之间的距离成正比

$F\propto {\frac {m_{1}m_{2}}{r^{2}}}$.

这种关系是牛顿万有引力定律通常表述的基础

任何两个点质量都相互吸引，吸引力与它们的质量成正比，与它们之间距离的平方成反比。

然而，要将其转化为一个方程，我们需要添加一个比例常数 G

$F=-G{\frac {m_{1}m_{2}}{r^{2}}}$.

其中 G 是**万有引力常数**，$6.67\times 10^{-11}\ \mathrm {N\cdot m^{2}\cdot kg^{-2}}$。方程中还有一个负号，这将在“电场”模块中解释，在那里我们将遇到排斥力和吸引力。

$F=-G{\frac {m_{1}m_{2}}{r^{2}}}$ 也有时写成 $F=-G{\frac {Mm}{r^{2}}}$，这样大写的 M 就代表行星这样的巨大质量，而小写的 m 就代表球或飞机这样的较小质量。

万有引力场强

定义万有引力场强

万有引力场强告诉我们万有引力场有多强。你可能还记得，地球表面附近的万有引力场强为 $9.81\,\mathrm {m/s^{2}}$。这意味着在地球表面附近的物体将以 $9.81\,\mathrm {m/s^{2}}$ 的加速度朝它加速。然后我们可以将万有引力场强定义为物体在该万有引力场中将经历的加速度。

然而，一个更好的定义可以从方程 $F=ma$ 推导出。使 $a$ 成为该方程的主体，我们得到 $a={\frac {F}{m}}$，或 $g={\frac {F}{m}}$。从这个方程的排列方式，我们对万有引力场强的定义现在变成了

某点处的万有引力场强是在该点放置的单位质量所受到的万有引力。

这意味着万有引力场强 $g$ 等于 1 kg 质量在该万有引力场中所受到的力。

从新的定义来看，万有引力场强是用 $\mathrm {N\ kg^{-1}}$ 测量的，虽然在将其视为加速度（如自由落体中的物体的加速度）的情况下，使用 $\mathrm {ms^{-2}}$ 是完全可以接受的。

求质量的场强

由于 $F=-G{\frac {Mm}{r^{2}}}$ 以及 $\ F=mg$，它们可以组合得到

$mg=-G{\frac {Mm}{r^{2}}}$ （将 F 替换为 mg）

$g=-G{\frac {M}{r^{2}}}$ （通过约去小写 'm'）

您可以使用此公式来求解特定点 r 处质量的重力场强度。

请注意，地球表面附近的重力场强度在数值上等于自由落体的加速度，$9.81\ \mathrm {ms^{-2}}$。