波/叠加

波 : 一维波
1 - 2 - 3 - 4 - 5 - 6 - 7 - 8 - 9 - 10 - 11 - 12 - 13
例子 - 问题 - 解决方案 - 术语

叠加原理

经验表明，只要大多数介质中波的振幅足够小，两个在同一物理位置的波就不会相互作用。因此，例如，两个向相反方向传播的波简单地穿过彼此，而不会改变它们形状或振幅。当叠加时，总波位移只是各个波位移的总和。这被称为叠加原理。在足够大的振幅下，叠加原理通常会失效——相互作用的波可能会互相散射、失去振幅或改变形状。

干涉是叠加原理的结果。当两个或多个波叠加时，净波位移只是各个波位移的代数和。由于这些位移可以是正或负的，因此净位移可以大于或小于各个波位移。前者称为相长干涉，而后者称为相消干涉。

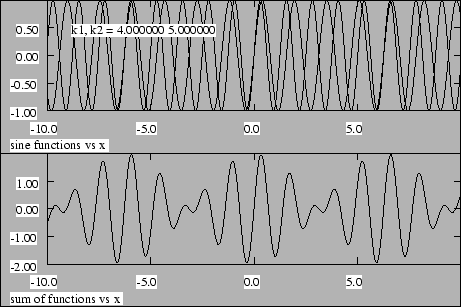
Figure 1.5: Superposition of two sine waves

图 1.5: 两个正弦波（分别显示在上图中）的叠加（下图），具有相同的振幅和波数

k_{1}=4

和

k_{2}=5

让我们看看当我们将两个波数不同的正弦波叠加时会发生什么。图 1.5 显示了波数为 $k_{1}=4$ 和 $k_{2}=5$ 的两个波的叠加。请注意，结果是一个波，其波长与两个初始波的波长大致相同，但振幅会根据两个正弦波是同相还是反相而变化。当波处于同相时，会发生相长干涉，而当波处于反相时，会发生相消干涉。

图 1.6: 两个正弦波的叠加
图 1.6: 两个正弦波的叠加，具有相同的振幅和波数

k_{1}=10

和

k_{2}=11

当两个正弦波的波数改变时会发生什么？图 1.6 显示了 $k_{1}=10$ 和 $k_{2}=11$ 时的情况。请注意，虽然结果波的波长减小了，但振幅最大的位置在 $x$ 上的间隔与图 1.5 中相同。

Figure 1.7: Superposition of two sine waves

图 1.7: 两个正弦波的叠加，具有相同的振幅和波数

k_{1}=10

和

k_{2}=12

.

如果我们将波叠加，其中 $k_{1}=10$ 和 $k_{2}=12$ ，如图 1.7 所示，我们会看到最大振幅区域的 $x$ 间距减少了一半。因此，虽然合成波的波数似乎与分量波的波数的平均值有关，但最大波幅区域之间的间距似乎与分量波的波数差值成反比。换句话说，如果 $k_{1}$ 和 $k_{2}$ 彼此接近，则振幅最大值相距很远，反之亦然。

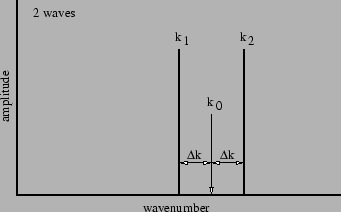
Figure 1.8: Representation of the wavenumbers and amplitudes of two superimposed sine waves.

图 1.8：两个叠加正弦波的波数和振幅的表示。

我们可以用类似图 1.8 所示的图来符号表示构成图 1.5、1.6 和 1.7 的正弦波。图中用垂直线表示每个正弦波的振幅和波数。

波幅较大的区域称为波包。波包将在随后的内容中发挥核心作用，因此我们必须对它们有很好的理解。仅由两个正弦波产生的波包在 $x$ 轴上没有很好地分离。但是，如果我们叠加许多波，我们可以产生一个孤立的波包。例如，图 1.9 显示了叠加 $20$ 个波数为 $k=0.4m$ ， $m=1,2,\ldots ,20$ 的正弦波的结果，其中波的振幅在波数接近 $k=4$ 时最大。

Figure 1.9: Superposition of twenty sine waves

图 1.9：叠加 20 个波数为

k_{0}=4

和

\Delta k=1

的正弦波。

特别是，我们假设每个正弦波的振幅与 $\exp[-(k-k_{0})^{2}/\Delta k^{2}]$ 成正比，其中 $k_{0}=4$ 和 $\Delta k=1$ 。构成图 1.9 中波包的每个正弦波的振幅在图 1.10 中以示意图形式表示。

Figure 1.10: Superposition of twenty sine waves

图 1.10：表示 20 个叠加正弦波的波数和振幅，其中

k_{0}=4

和

\Delta k=1

。

量 $\Delta k$ 控制着叠加正弦波的分布——只有波数在中心波数 $k_{0}$ 附近大约 $\Delta k$ 范围内的那些波，即在这个例子中 $3\leq k\leq 5$ ，对总和有显著贡献。如果 $\Delta k$ 改变为 $2$ ，使得 $2\leq k\leq 6$ 范围内的波数对总和有显著贡献，波包会变得更窄，如图 1.11 和 1.12 所示。

Figure 1.11: Superposition of twenty sine waves

图 1.11：二十个正弦波的叠加，其中

k_{0}=4

且

\Delta k=2

。

Figure 1.12: Superposition of twenty sine waves

图 1.12：表示 20 个叠加的正弦波的波数和振幅，其中

k_{0}=4

且

\Delta k=2

。

$\Delta k$ 被称为波包的波数扩展，它显然起着类似于两个正弦波叠加中波数差的作用——波数扩展越大，波包的物理尺寸越小。此外，波包内振荡的波数近似等于中心波数。

通过数学分析两个正弦波叠加的简单情况，我们可以更好地理解波包是如何工作的。让我们定义 $k_{0}=(k_{1}+k_{2})/2$ ，其中 $k_{1}$ 和 $k_{2}$ 是组成波的波数。此外，让我们设置 $\Delta k=(k_{2}-k_{1})/2$ 。图 1.8 图示了 $k_{0}$ 和 $\Delta k$ 。我们可以写 $k_{1}=k_{0}-\Delta k$ 和 $k_{2}=k_{0}+\Delta k$ ，并使用三角恒等式 $\sin(a+b)=\sin(a)\cos(b)+\cos(a)\sin(b)$ 来找到 $\sin(k_{1}x)+\sin(k_{2}x)=\sin[(k_{0}-\Delta k)x]+\sin[(k_{0}+\Delta k)x]$ $=\sin(k_{0}x)\cos(\Delta kx)-\cos(k_{0}x)\sin(\Delta kx)+$ $\sin(k_{0}x)\cos(\Delta kx)+\cos(k_{0}x)\sin(\Delta kx)=2\sin(k_{0}x)\cos(\Delta kx).$ (2.17)