工程声学/吸声结构和材料

介绍

噪声可以定义为不需要的声音。在许多情况下和应用中，降低噪声水平非常重要。听力损失只是持续暴露于过高噪声水平的其中一个影响。噪声会干扰睡眠和说话，并造成不适和其他非听觉影响。此外，高水平的噪声和振动会导致许多工业设备的结构故障以及使用寿命缩短。例如，在控制阀中，由流动不稳定引起的振动有时会损坏控制系统的反馈，从而导致极端的振荡。通过观察政府为了限制社会噪声排放而制定的法规，可以很好地理解噪声问题的重要性。工业机械、空/陆地交通运输和建筑活动被认为是噪声产生或所谓的“噪声污染”的主要贡献者。

噪声控制机制

• 主动噪声控制

通过电声方法修改和消除声场称为主动噪声控制。主动控制有两种方法。第一种是利用执行器作为声源产生完全异相信号以消除干扰。第二种方法是使用柔性和振动弹性材料来辐射干扰干扰的声场并最小化整体强度。后一种方法称为主动结构声学控制 (ASAC)。

• 被动噪声控制

被动噪声控制是指那些通过修改靠近声源的环境来抑制声音的方法。由于此类方法不需要输入功率，因此被动噪声控制通常比主动控制更便宜，但性能仅限于中高频。主动控制在低频工作良好，因此可以将两种方法结合起来用于宽带噪声抑制。

图 1：噪声控制机制

吸声

声波撞击任意表面时，会发生反射、透射或吸收；进入反射、透射或吸收的能量多少取决于表面的声学特性。反射声可以被大的平坦表面几乎完全地重新定向，也可以被漫反射表面散射。当大量反射声在空间和时间上发生散射时，这种状态称为漫反射，涉及的表面通常称为漫射器。吸收的声能可以被透射或消散。图 2 显示了表面-波相互作用的简单示意图。

图 2：表面-声相互作用 - 吸收（左）、反射（中）和漫射（右）

声能通过粘性和热机制的共同作用而消散。吸声器用于消散声能，以最大程度地减少其反射。 吸声系数 $\alpha$ 是一个常用的测量材料吸声性能的量，已知它是入射波频率的函数。它被定义为材料吸收的能量与入射到其表面的能量之比。

吸声系数

吸声系数可以数学表达如下

$\alpha =1-{\frac {I_{R}}{I_{I}}}$

其中 α，$I_{R}$ 和 $I_{I}$ 分别代表吸声系数、反射声的单边强度和入射声的单边强度。

从上面的公式可以看出，材料的吸声系数在 0 到 1 之间变化。有几种标准方法可以测量吸声系数。在一种常用的方法中，使用配备了两个麦克风的平面波阻抗管。实验装置和尺寸符合 ASTM E1050/ISO 10534-2。 （图 3）该方法通过评估传递函数， ${\hat {h}}(f)$ 在两个相隔 s 的麦克风之间，以及从样品到麦克风的距离 l 来获得吸声系数，使用以下公式

${\hat {h}}={\frac {\hat {p_{1}}}{\hat {p_{2}}}}$

${\hat {r}}={\frac {{\hat {h}}-e^{-jks}}{e^{jks}+{\hat {h}}}}$

$\alpha =1-|{\hat {r}}|^{2}$

其中，${\hat {p_{1}}},{\hat {p_{2}}}$ 分别是麦克风 1 和麦克风 2 测量的复压振幅。k 是波数，s 是麦克风的间距，$\alpha$ 是吸声系数。

根据标准技术， 频率受麦克风间距和管径的限制。还建议 $0.05{\frac {c}{s}}<f<0.45{\frac {c}{s}}$ 以确保平面波传播。商业吸声材料的系数以噪声衰减系数 (NRC) 表示，指的是 250 Hz、500 Hz、1000 Hz 和 2000 Hz 吸声系数的平均值。表 1 列出了建筑物中使用的一些声学隔音材料的平均值。根据其结构和材料结构，吸声器分为 非多孔 和 多孔 吸声器。

图 3：双麦克风法获得吸声系数

表 1 - 常用吸声材料的吸声系数

材料	吸声系数
6 毫米软木板	0.1-0.2
6 毫米多孔橡胶板	0.1-0.2
12 毫米纤维板	0.3-0.4
50 毫米矿渣棉或玻璃丝	0.8-0.9
硬木	0.3
100 毫米矿棉	0.65

非多孔吸声器（吸声共振器）

在工业应用中，有两种常见的非多孔吸声器。面板（膜）共振器 和 亥姆霍兹共振器。面板吸声器是轻质、薄而没有孔洞的板材或膜，这些板材或膜经过调谐，可以在特定频率范围内吸收声波。面板对快速成形的结构阻力导致吸声。面板吸声器由其几何形状和结构振动特性决定。亥姆霍兹共振器或腔体吸声器是具有非常小孔的穿孔结构；一个例子是用于飞机发动机机架内部的吸声衬层，用于抑制压缩和燃烧阶段产生的噪声排放。类似的结构应用于通风和空调系统中使用的风机和通风机。开口尺寸、颈部长度和腔体体积决定了共振器的共振频率，因此也决定了吸声性能。

多孔吸声器

多孔吸声器对应于声波在相互连接的孔隙网络中传播的材料，因此粘性热相互作用导致声能耗散并转化为热能。矿渣棉、玻璃纤维或高孔隙率泡沫等吸声处理可减少反射声。多孔吸声器实际上是热工材料，通常不是有效的隔音屏障。与工作声波长相比，需要相当大的厚度，这使得多孔吸声器在低频时效率低下且不切实际。

图 2：不同吸声体吸声系数的典型变化

多孔吸声体的物理特性

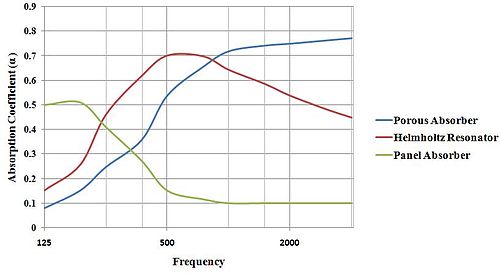
声音在多孔材料中的传播是一个受多孔介质物理特性控制的现象，即孔隙率 ($\phi$)、曲折度 (q)、流动阻抗 ($\sigma$)、粘性特征长度 ($\Lambda$) 和热特征长度 ($\Lambda '$).

• 孔隙率

定义为相互连通的空隙体积（开放孔隙中的空气体积）与总体积的比率。大多数商业吸声体具有高孔隙率（大于 0.95）。孔隙率越高，固体-流体相之间的相互作用就越容易，从而导致更多的声能衰减。

$\phi ={\frac {V_{0}}{V_{T}}}$

$V_{0}$ = 空隙空间的体积。

$V_{T}$ = 多孔材料的总体积。

• 曲折度

该物理特性对应于多孔材料内部孔隙网络的“非直线性”。它显示了多孔材料如何有效地阻止穿过多孔介质的直接流动。路径越复杂，波与吸声体接触的时间就越长，因此能量耗散越多，吸声能力就越强。如果多孔吸声体不导电，一种测量方法是将吸声体浸泡在导电流体中并测量饱和样品的电阻率，$R_{s}$，并与流体本身的电阻率进行比较，$R_{f}$，则曲折度可以表示如下

$q=\phi {\frac {R_{s}}{R_{f}}}$

• 流动阻抗

驱动单位流量通过材料所需的压降可以与多孔吸声体内传播声波的粘性损失相关联，并表示为流动阻抗。对于各种多孔材料，流动阻抗是声吸收的主要因素。流动阻抗的单位是 $N.s/m^{4}$ 或 $Rayls/m$，定义为静态压降 $\Delta P$ 与体积流量 (U) 的比值，对于小的样品厚度 (d)。

$\sigma ={\frac {\Delta P}{Ud}}$

• 特征长度

另外两个重要的微观结构特性是特征粘性长度$\Lambda$和特征热长度$\Lambda$’，它们分别导致粘性耗散和热耗散。前者与较小的孔隙相关，后者与多孔聚集体的较大孔隙相关。热长度$\Lambda '$是连通孔隙中体积与表面积之比的两倍。它是一个几何量，可以直接测量。粘性长度，$\Lambda$，几乎相同，但每个积分都乘以孔隙内流体速度v的平方，因此无法直接测量。

$\Lambda '=2{\frac {\int dV}{\int dS}}$

$\Lambda =2{\frac {\int v_{fluid}^{2}dV}{\int v_{fluid}^{2}dS}}$

多孔吸声材料的声学建模

刚性多孔吸声材料中的波动方程

从质量守恒和动量守恒的线性化方程推导的平面波方程应该修改，以考虑孔隙率、曲折度和流动阻力的影响。修改后的波动方程控制着可压缩气体填充的刚性多孔材料中的声传播，其表达式为

${\frac {\partial ^{2}P}{\partial x^{2}}}-({\frac {q\rho _{0}}{k_{eff}}})*{\frac {\partial ^{2}P}{\partial t^{2}}}-({\frac {\sigma \phi }{k_{eff}}})*{\frac {\partial p}{\partial t}}=0$

其中，p = 材料孔隙内的声压

$\rho _{0}$ = 可压缩气体的密度

$k_{eff}$ = 气体的有效体积模量

q = 曲折度

$\phi$ = 孔隙率

$\sigma$ = 流动阻力

吸声多孔层的声学特性也可以从其基本声学量进行研究：复波数和特征阻抗。这些量是作为修改后的平面波方程解的一部分获得的，可用于确定吸声系数和表面阻抗。复波数和表面阻抗最实用和最常见的值基于半经验方法，并使用回归分析进行关联。Delany 和 Bazely 建议了一种重要的关联

$k'=\alpha +j\beta ={\frac {\omega }{c}}[1+0.0978({\frac {\rho _{0}f}{\sigma }})^{-0.700}-j0.189({\frac {\rho _{0}f}{\sigma }})^{-0.595}]$

$z'=R+jX=\rho _{0}c[1+0.0571({\frac {\rho _{0}f}{\sigma }})^{-0.754}-j0.087({\frac {\rho _{0}f}{\sigma }})^{-0.732}]$

其中，f = 频率 σ = 流阻

有效密度

假设吸声材料的孔隙网络为刚性框架，固体相完全静止，框架体积模量远大于可压缩气体的体积模量，因此可以使用具有复杂有效流体密度和复杂有效体积模量的流体波动方程对其进行建模。在这种情况下，动态密度考虑了粘性损耗，而动态体积模量考虑了热损耗。Johnson 等人提出了有效密度与动态曲折度的关系。

$\rho _{eff}=q(1+{\frac {\sigma \phi }{j\omega \rho _{0}q}}G(\omega ))\rho _{0}$

$G(\omega )={\sqrt {1+j{\frac {4q^{2}\mu \rho _{0}\omega }{\sigma ^{2}\Lambda ^{2}\phi ^{2}}}}}$

其中，

μ = 气体粘度

ω = 2πf

有效体积模量

另一个影响吸声材料中声传播的因素是材料中的热相互作用，这是由于可压缩流体中传播的声波前沿与固体相之间的热交换造成的。Champoux 和 Allard .，引入了函数 $G'(\omega )$ 来评估气体的有效体积模量。正如在下面的公式中观察到的那样，这将是热特征长度 ($\Lambda '$).

$k_{eff}={\frac {\gamma p_{0}}{\gamma -(\gamma -1)(1-j{\frac {8\mu }{\Lambda '^{2}Pr^{2}\omega \rho _{0}}}G'(\omega ))\rho _{0}}}$

$G'(\omega )={\sqrt {1+j{\frac {\Lambda '^{2}Pr^{2}\omega \rho _{0}}{16\mu }}}}$

其中，

γ = 气体比热比（对于空气约为 1.4）

Pr = 流体普朗特数