工程声学/换能器 - 扬声器

声学换能器

声学换能器的目的是将电能转换为声能。声学换能器有很多变体，例如静电式、动铁式和动圈式扬声器。本文重点介绍动圈式扬声器，因为它们是最常用的声学换能器类型。首先，简要讨论了典型的动圈式换能器的物理结构和原理。其次，以教程的方式介绍了组成扬声器的每个元素的机电声建模，以加强和补充之前在其他部分中看到的关于机电模拟和机声模拟的理论。第三，分析了等效电路，引入了Thiele-Small 参数背后的理论，这些参数在设计扬声器箱体时非常有用。还包括了一种实验确定 Thiele-Small 参数的方法。

动圈式扬声器结构和原理

经典的动圈式扬声器驱动器可以分为三个关键部分

1）磁电机系统，包括永磁体、中心极和音圈，它们共同作用，通过电流在振膜上产生机械力。

2）扬声器锥盆系统，包括振膜和防尘罩，使机械力转换为声压；

3）扬声器悬挂系统，包括蜘蛛和环绕，防止振膜因过度偏移而破裂，只允许平移运动，并倾向于使振膜回到其静止位置。

以下插图显示了一个典型的动圈式永磁扬声器的剖视图。一个线圈机械地耦合到一个振膜（也称为锥盆），并位于由磁铁产生的固定磁场中。当电流流过线圈时，会发出相应的磁场，与磁铁的固定场相互作用，从而对线圈施加力，将其推离或朝向磁铁。由于锥盆与线圈机械耦合，它将推或拉动它所面对的空气，导致压力变化并发出声波。

图 1：典型的动圈式扬声器的横截面图

可以获得一个等效电路来对扬声器进行建模，使其成为一个集总系统。该电路可用于驱动完整扬声器系统的设计，包括箱体，有时甚至与驱动器特性匹配的放大器。下一部分展示了如何获得这种等效电路。

机电声等效电路

只要每个元素作为一个整体运动，像扬声器这样的机电声系统就可以建模为等效电气电路。这在低频或系统尺寸远小于感兴趣波长的情况下通常是正确的。为了获得扬声器的完整模型，必须对组成扬声器驱动器的电气、机械和声学子系统之间的相互作用和特性进行建模。以下部分详细介绍了如何从放大器开始，到空气呈现的声学负载结束，获得该电路。类似的推导可以在[1]或[2]中找到。

电气子系统

系统中的电气部分由驱动放大器和音圈组成。大多数放大器可以近似为串联在放大器输出阻抗中的理想电压源。音圈表现出电感和电阻，可以作为电路直接建模。

图 2：放大器和扬声器电气元件作为电路建模

电气到机械子系统

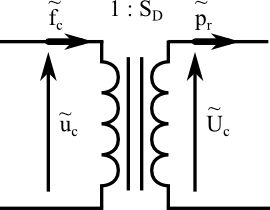
当扬声器接收到电信号时，音圈和磁铁将电流转换为力。类似地，电压与速度相关。这种电气侧与机械侧之间的关系可以用一个变压器来建模。

${\tilde {f_{c}}}=Bl{\tilde {i}}$; ${\tilde {u_{c}}}={\dfrac {\tilde {e}}{Bl}}$

图 3：将转换从电阻抗建模为机械迁移率类比的变压器

机械子系统

在最初的近似中，动圈式扬声器可以被认为是一个质量-弹簧系统，其中振膜和音圈构成质量，蜘蛛和悬边构成弹簧元件。悬挂中的损耗可以建模为一个电阻。

图 4：阻抗和迁移率类型的质量弹簧系统和相关电路类比。

运动方程给出我们 

${\tilde {f_{c}}}=R_{m}{\tilde {u_{c}}}+{\dfrac {\tilde {u_{c}}}{j\omega C_{MS}}}+j\omega M_{MD}{\tilde {u_{c}}}$ ${\dfrac {\tilde {f_{c}}}{\tilde {u_{c}}}}=R_{m}+{\dfrac {1}{j\omega C_{MS}}}+j\omega M_{MD}$

这产生了以串联 RLC 电路形式的机械阻抗类型类比。还可以通过数学操作获得并联 RLC 电路以获得迁移率类比

${\dfrac {\tilde {u_{c}}}{\tilde {f_{c}}}}={\dfrac {1}{R_{m}+{\dfrac {1}{j\omega C_{MS}}}+j\omega M_{MD}}}$ ${\dfrac {\tilde {u_{c}}}{\tilde {f_{c}}}}={\dfrac {1}{{\dfrac {1}{G_{m}}}+{\dfrac {1}{j\omega C_{MS}}}+{\dfrac {1}{\dfrac {1}{j\omega M_{MD}}}}}}$

这表示以并联 RLC 电路形式的机械迁移率类型类比，其中分母元素分别是并联电导、电感和顺从性。

机械到声学子系统

扬声器的振膜可以被认为是一个活塞，它对它所面对的空气进行推拉，将机械力和速度转换为声压和体积速度。方程如下：

${\tilde {P_{d}}}={\dfrac {\tilde {f_{c}}}{\tilde {S_{D}}}}$; ${\tilde {U_{c}}}={\tilde {u_{c}}}{S_{D}}$

这些方程可以用一个变压器来模拟。

图 5: 模拟扬声器振膜执行的从机械移动性到声学移动性类比的变换的变压器。

声学子系统

扬声器振膜上的空气负载呈现的阻抗既有由于声音辐射引起的电阻性阻抗，也有由于正在径向推动但没有对远场声音辐射做出贡献的空气质量引起的电抗性阻抗。振膜上的空气负载可以用阻抗或导纳来模拟。在 [1]、[2] 或 [3] 中可以找到特定值和近似值。请注意，空气负载取决于扬声器的安装条件。如果扬声器安装在挡板上，则振膜两侧的空气负载将相同。然后，如果一侧的空气负载是 $Y_{AR}$ 在导纳类比中，那么总空气负载就是 $Y_{AR}/2$，因为两个负载都是并联的。

完整的电-机-声等效电路

使用电阻抗、机械移动性和声学导纳，可以得到以下等效电路，该电路模拟整个扬声器驱动单元。

图 6: 扬声器驱动单元的完整电-机-声等效电路。

可以通过用与负载变压器具有相同阻抗的等效负载替换变压器和连接的负载来简化该电路。图 7 显示了这一点的一个例子，其中声学和电气负载和电源已“转移”到机械侧。

图 7: 扬声器驱动单元的机械等效电路建模。

这样做的好处是，我们可以直接将电气测量值与电路中的元素相关联。这将使我们能够随后获得模型不同组件的值，并将该模型与实际扬声器驱动器匹配。我们可以通过使用诺顿定理并将串联电气元件和电压源转换为等效电流源和并联电气元件来进一步简化该电路。然后，使用称为“点法”的技术（在 解决方案方法：电-机械类比 部分介绍），我们可以得到一个单环串联电路，它是先前使用诺顿定理获得的并联电路的对偶。如果我们主要对扬声器的低频行为感兴趣，就像使用集中元件建模时应该的那样，我们可以忽略音圈电感的效应，该电感仅在高频下才有效应。此外，低频下的空气负载阻抗类似于质量，可以用一个简单的电感 $M_{M1}$ 来模拟。这将导致一个简化的低频模型等效电路（如图 8 所示），它比图 7 中的电路更容易操作。请注意，此电路使用的类比是阻抗类型的。

图 8: 扬声器驱动单元的低频近似机械等效电路。

其中 $M_{M1}=2.67a^{3}\rho$ 如果 $a$ 是扬声器的半径，而 $\rho$ 是空气的密度。在这种情况下，振膜和音圈的质量 $M_{MS}$ 和对振膜进行空气质量负载的 $2M_{M1}$ 可以合并到一个元素中。

$M_{MS}=M_{MD}+2M_{M1}$

Thiele-Small 参数

理论

扬声器驱动单元的完整低频行为可以用六个参数建模，称为 Thiele-Small 参数。这些参数中的大多数是来自图 8 电路的方程的代数运算结果。扬声器驱动器制造商很少直接提供机电声参数，而是会在数据表中提供 Thiele-Small 参数，但从一种参数转换到另一种参数非常简单。Thiele-Small 参数如下所示

1. $R_{e}$，音圈直流电阻；

2. $Q_{ES}$，电气品质因数；

3. $Q_{MS}$，机械品质因数；

4. $f_{s}$，扬声器谐振频率；

5. $S_{D}$，振膜的有效表面积；

6. $V_{AS}$，等效悬挂体积：与扬声器驱动器的悬挂具有相同声学顺应性的空气体积。

这些参数可以直接从图 8 的低频近似电路中关联，其中 $R_{e}$ 和 $S_{D}$ 是明确的。

$Q_{MS}={\dfrac {1}{R_{MS}}}{\sqrt {\dfrac {M_{MS}}{C_{MS}}}}$； $Q_{ES}={\dfrac {R_{g}+R_{e}}{(Bl)^{2}}}{\sqrt {\dfrac {M_{MS}}{C_{MS}}}}$ ; $f_{s}={\dfrac {1}{2\pi {\sqrt {M_{MS}C_{MS}}}}}$； $V_{AS}=C_{MS}S_{D}^{2}\rho c^{2}$

其中 $\rho c^{2}$ 是空气的体积模量。因此，如果给定了 Thiele-Small 参数，则可以使用以下公式提取图 8 电路中每个组件的值

$C_{MS}={\dfrac {V_{AS}}{S_{D}^{2}\rho c^{2}}}$; $M_{MS}={\dfrac {1}{(2\pi f_{s})^{2}C_{MS}}}$; $R_{MS}={\dfrac {1}{Q_{MS}}}{\sqrt {\dfrac {M_{MS}}{C_{MS}}}}$; $Bl={\sqrt {\dfrac {R_{e}}{2\pi f_{s}Q_{ES}C_{MS}}}}$; $M_{MD}=M_{MS}-2M_{M1}$;

测量

许多方法可以用来测量驱动器的Thiele-Small参数。如果制造商没有提供Thiele-Small参数，有时需要测量。此外，给定扬声器的实际Thiele-Small参数可能与标称值存在显著差异。本节中描述的方法来自[2]。请注意，对于此方法，扬声器被认为是安装在无限大的挡板上。在实践中，直径为扬声器直径四倍的挡板就足够了。也可以在没有挡板的情况下进行测量：空气质量负载只会减少一半，并且可以轻松地进行调整。此方法的设置包括一个FFT分析仪或用于获取阻抗曲线的工具。也可以使用可变频率的信号发生器和交流表。

图9：测量扬声器驱动单元阻抗的简单实验装置 $Z_{spk}=R{\dfrac {V_{spk}}{V_{s}\left(1-{\dfrac {V_{spk}}{V_{s}}}\right)}}$ 图10：典型的扬声器驱动单元阻抗曲线

一旦测量了扬声器的阻抗曲线，$R_{e}$ 和 $f_{s}$ 可以通过观察阻抗值的低频渐近线和共振峰的中心频率来直接识别。如果识别出 $Z_{spk}={\sqrt {R_{e}R_{c}}}$ 的频率为 $f_{l}$ 和 $f_{h}$，可以计算出Q因子。

$Q_{MS}={\dfrac {f_{s}}{f_{h}-f_{l}}}{\sqrt {\dfrac {R_{c}}{R_{e}}}}$ $Q_{ES}={\dfrac {Q_{MS}}{{\dfrac {R_{c}}{R_{e}}}-1}}$

$S_{D}$ 可以简单地用 $\pi a^{2}$ 近似，其中 $a$ 是扬声器驱动器的半径。最后一个剩余的 Thiele-Small 参数，$V_{AS}$ 测量起来稍微棘手一点。想法是增加扬声器驱动单元的质量或降低其顺性，并记录共振频率的变化。如果已知的质量 $M_{x}$ 添加到扬声器振膜上，新的共振频率将是

$f_{s}^{'}={\dfrac {1}{2\pi {\sqrt {(M_{MS}+M_{x})C_{MS}}}}}$

等效悬挂体积可以通过以下方法获得

$V_{AS}=\left(1-{\dfrac {f_{s}^{'2}}{f_{s}^{2}}}\right){\dfrac {S_{D}^{2}\rho c^{2}}{(2\pi f_{s}^{'})^{2}M_{x}}}$

因此，所有用于模拟扬声器驱动单元低频特性的 Thiele-Small 参数都可以从一个相当简单的设置中获得。这些参数在扬声器箱体设计中起着至关重要的作用。

数值示例

本节介绍了从阻抗曲线获取 Thiele-Small 参数的数值示例。本节中提供的阻抗曲线是使用真实低音扬声器的标称 Thiele-Small 参数通过仿真获得的。首先，这些 Thiele-Small 参数使用之前介绍的方程转换为电-机-声电路。其次，该电路被视为黑盒子，并使用了提取 Thiele-Small 参数的方法。该仿真的目的是使用实际值逐步展示该方法，以便读者能够更加熟悉该过程、值的大小以及执行此类测量时应期望的结果。

在本仿真中，半径为 $a=6.55cm$ 的扬声器安装在足够大的挡板上，以充当无限挡板。其阻抗被获得并绘制在图 11 中，其中重要的光标已经放置。

图 11：低音扬声器阻抗曲线的仿真测量

低频渐近线立即被识别为 $Re=6.6\Omega$。共振清晰，位于 $fs=33Hz$。该频率下的阻抗值约为 $66\Omega$。这产生了 ${\sqrt {R_{e}R_{c}}}=20.8\Omega$，它出现在 $f_{l}=19.5Hz$ 和 $f_{h}=52.5Hz$。有了这些信息，我们可以计算一些 Thiele-Small 参数。

$Q_{MS}={\dfrac {f_{s}}{f_{h}-f_{l}}}{\sqrt {\dfrac {R_{c}}{R_{e}}}}={\dfrac {33}{52.5-19.5}}*{\sqrt {\dfrac {66}{6.6}}}=3.1$ $Q_{ES}={\dfrac {Q_{MS}}{{\dfrac {R_{c}}{R_{e}}}-1}}={\dfrac {3.1}{{\dfrac {66}{6.6}}-1}}=0.35$

下一步，将质量为 $M_{x}=10g$ 的物体固定在扬声器振膜上。这将改变共振频率，并产生新的阻抗曲线，如图 12 所示。

图 12：低音扬声器阻抗曲线的模拟测量 $S_{D}=\pi a^{2}=0.0135m^{2}$ $V_{AS}=\left(1-{\dfrac {27.5^{2}}{33^{2}}}\right){\dfrac {0.0135^{2}*1.18*344^{2}}{(2\pi 27.5)^{2}*0.01}}=0.0272m^{3}$

一旦获得所有六个 Thiele-Small 参数，就可以计算图 6 或 7 中电机械声学电路模型元素的值。然后，就可以开始设计音箱。这将在应用部分 密封箱低音炮设计 和 低音反射箱设计 中讨论。

参考文献

[1] Kleiner，Mendel。电声学。CRC 出版社，2013 年。

[2] Beranek，Leo L. 和 Tim Mellow。声学：声场和换能器。学术出版社，2012 年。

[3] Kinsler，Lawrence E. 等。声学基础，第 4 版。Wiley-VCH，1999 年。

[4] Small，Richard H. “直接辐射扬声器系统分析”。《音频工程学会期刊》20.5 (1972)：383-395。