几何/第 16 章

作图是指用圆规和直尺来构造图形（例如正方形、角平分线等）。

构造与给定线段全等的线段

要构造与给定线段全等的线段，将圆规设定到给定线段的两端点。然后从第二条直线上的一个起点开始，用圆规标记相同的距离。此线段与给定线段全等。

等边三角形

作图的一个例子是用两个相交圆来构造等边三角形。用相同的半径绘制两个圆，使每个圆上的一点与另一个圆的半径相交。

然后从半径到两个圆的交点，以及两个半径之间画线。

现在我们得到了一个等边三角形。

角平分线

构造角平分线的方法：1. 将圆规的中心放在角上，并在每条线上标记一个交点。

2. 将圆规的中心放在一个标记的交点上，然后在中心附近标记两个点。在另一个交点上重复此步骤。

3. 画一条线连接两个交点和角。

垂直平分线

要构造给定线段 AB 的垂直平分线，首先以点 A 为中心画一个圆。然后用圆规以点 B 为中心画一个与第一个圆半径相同的圆。最后，连接两个圆的交点，称为 C 和 D。这条线段就是垂直平分线。推理：任何与线段端点等距的点都位于该线段的垂直平分线上。给出两个这样的点，你就可以画出这条线。

Image:PerpendicularBisector2JPEG.jpg

构造与给定角全等的角

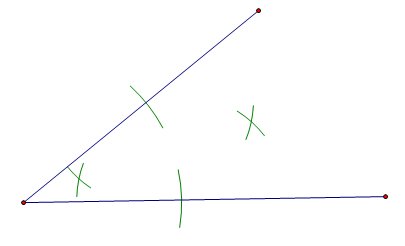
要构造与给定角全等的角，首先在你要构造全等角的线段上画一条线段。在这条线段上标记一个点，这个点将作为新全等角的顶点。画一条弧（圆的一部分）穿过原始角的两边。然后用与这条弧相同的设定，从线段上的点开始画一条弧，使这条弧与前一条弧的半径相同。接下来，用圆规测量第一条弧与角两边的交点之间的距离。现在，以相同的设定到第二条弧，在第二条弧上标记与第一条弧相同的距离。将此点与线段上的原始点连接起来。

过直线上一点作这条直线的垂线

给定直线上的一点，首先以该点为中心画一个圆。用圆与直线的两个交点画出两个全等的弧，它们相互相交。这个点与圆的两个端点等距，因此在它的垂直平分线上，原始点也一样。连接这两个点以完成构造。

过直线外一点作这条直线的垂线

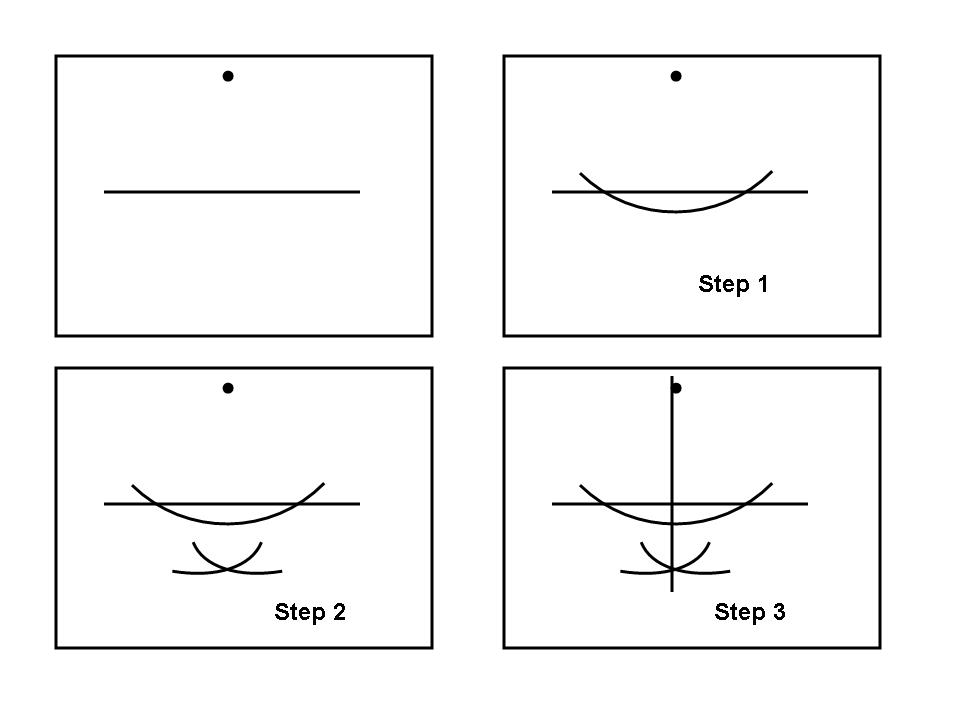
要过直线外一点作这条直线的垂线，以该点为圆心画一条弧，与直线相交于两点。你的原始点将位于由这两个新点形成的线段的垂直平分线上。用这两个点为中心画出两个全等的弧，它们相互相交，你就可以得到该垂直平分线上的另一个点。将这个新点与你的原始点连接起来以完成这个构造。

构造与给定三角形全等的三角形（SSS 方法）

要构造与给定三角形全等的三角形，首先以与构造全等线段相同的方式构造一条底边。用圆规测量给定三角形的第二边，然后从构造的线段的一端画一条弧。将圆规设定为给定三角形的第三边的长度，然后到构造的线段的第二点，画出另一条半径与第三边相同的弧，与第一条弧相交。将此交点与构造的线段的端点连接起来以完成全等三角形。