几何/附录 C

A

锐角

参见 角

等式的代数性质

对于实数 a、b 和 c

加法等式性质：如果 a=b ，则 a+c=b+c

减法等式性质：如果 a=b ，则 a-c+=b-c

乘法等式性质：如果 a=b，则 ac=bc

除法等式性质：如果 a=b 且 c≠0 ，则 (a/c)=(b/c)

对称等式性质：如果 a=b，则 b=a

传递等式性质：如果 a=b 且 b=c ，则 a=c

自反等式性质：如果 a=a ，则 a=a

代入等式性质：如果 a=b，则 a 可以代入 b

分配等式性质：a(b+c)=ab+ac

角

角 ABC 是锐角。

一个图形是角当且仅当它由两条具有共同端点的射线组成。每条射线（或线段，视情况而定）被称为角的边（例如，${\overline {AB}}\;$在右侧的图示中），共同点被称为角的顶点（图示中的点B）。角的度量由它们的斜率差决定。角度量的单位是弧度和度数。角可以按其度数分类。

• 锐角：一个角是锐角当且仅当它的度数小于 90°
• 直角：一个角是直角当且仅当它的度数正好为 90°
• 钝角：一个角是钝角当且仅当它的度数大于 90°
• 平角：一个角是平角当且仅当它的度数正好为 180°

使用直角全等定理和平角全等定理，所有直角和所有平角都是全等的。

角加法公理

如果 P 在角 $\angle ABC$ 的内部，则 $\angle ABC=\angle ABP+\angle PBC$

算术平均数

2 个数字 a 和 b 的算术平均数可以计算为：算术平均数=(a+b)/2

B

角平分线

一个图形平分另一个图形当且仅当它将它所相交的图形分成两个相等的部分。

C

圆心

点P 是圆C 的圆心当且仅当圆C 中的所有点与点P 等距，且点P 与圆C 在同一平面上。

圆

平面上所有与给定点（称为圆心）等距的点的集合。

周长

圆的周围距离。

它计算为

C=2πr（其中r是圆的半径）

余角

两个角互余当且仅当它们的度数之和等于90度。

凹

一个多边形被称为凹多边形当且仅当它至少包含一个内角，其度数大于180°且小于360°。

全等

两个图形全等当且仅当它们具有相同的度量。它用“≅”表示。

对应角

有四对对应角：∠1 和 ∠3、∠2 和 ∠4、∠5 和 ∠7、∠6 和 ∠8。

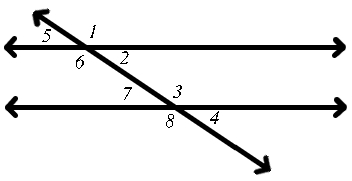
两条线被一条横截线所截而形成的两个角是对应角当且仅当一个角在两条线的内部，另一个角在两条线的外部，且它们都在横截线的同一侧。

对应角定理

如果两条线被一条横截线所截而平行，那么它们的对应角全等。

全等三角形的对应边和对应角全等定理

全等三角形的对应边和对应角全等定理 (CPCTC) 说明

如果 ∆ABC ≅ ∆XYZ，那么 ∆ABC 的所有部分都与其在 ∆XYZ 中的对应部分全等。例如

• ${\overline {AB}}\;$ ≅ ${\overline {XY}}\;$

• ${\overline {BC}}\;$ ≅ ${\overline {YZ}}\;$

• ${\overline {AC}}\;$ ≅ ${\overline {XZ}}\;$

• ∠ABC ≅ ∠XYZ

• ∠BCA ≅ ∠YZX

• ∠CAB ≅ ∠ZXY

CPCTC 也适用于三角形的其他所有部分，例如三角形的高、中线、外心等。

余弦

一个三角函数，缩写为cos。

cos(θ)=邻边/斜边

D

直径

一条线段是圆的直径当且仅当它是一个包含圆心的圆的弦。

参见 圆

距离

两点之间的距离可以计算为这两点坐标差的绝对值。

在坐标系中，点 A(x₁,y₁) 和 B(x₂,y₂) 之间的距离可以计算为

d(AB)=√((y₂-y₁)²+(x₂-x₁)²)

点和线之间的距离通过连接这两者（使用垂直定理）的垂直线段来衡量。

G

几何平均数

对于两个正数 a 和 b，a 和 b 的几何平均数是满足 (a/x)=(x/b) 的正数 x。因此，x²=√(ab)

a 和 b 的几何平均数 = (a/x)=(x/b) : x²=√(ab)

H

平行四边形的高度

平行四边形两底之间的垂直距离

斜边

在直角三角形中，与直角相对的边。

利用勾股定理，可以计算斜边的长度

c²=a²+b²（其中 c 是斜边，a 和 b 是直角三角形的两条直角边）

L

直线

当且仅当点集是完全直的（对齐）、无限长且无限薄时，点集才是一条直线。在线上的任意两点之间，都存在无限多个也被该直线包含的点。直线通常用直线上两点来表示，例如直线 AB，或 ${\overleftrightarrow {AB}}$

线段

线段 MN

当且仅当点集是完全直的、无限薄且具有有限长度时，点集才是一条线段。线段的长度由线段上两个极点（称为端点）之间的最短距离来衡量。在线段上的任意两点之间，都存在无限多个也被该线段包含的点。

I

正多边形的内角

正多边形的内角都是全等的。因此，具有 n 条边的正多边形的一个内角的度数可以计算为

内角 = ((n-2)180)/n

等腰梯形

两条腰相等的梯形。

等腰三角形

至少有两条边相等的三角形。

利用底角定理，与全等边相对的角也全等。

L

线性对

相邻的角，其非公共边是相反射线。

根据线性对公理，线性对中的角也是互补的。

如果构成线性对的两个角全等，那么这两个角都是直角，并且包含这两个角的直线是垂直的。

M

优弧

度数大于 180 度的弧。它必须由 3 个点命名。

梯形的 中线

连接梯形两腰中点的线段。

它平行于底边，其长度是两底长度的算术平均数。

劣弧

度数小于 180 度的弧。

P

平行线

当且仅当两条直线或线段被包含在同一个平面上，并且当无限延长时没有公共点，它们就被称为平行。

在坐标系中，两条直线平行当且仅当它们具有相同的斜率。

平行平面

当且仅当两个平面无限延长时没有公共点，这两个平面就被称为平行。

垂直线

在 90° 角处相交的两条直线。

在坐标系中，两条直线垂直当且仅当它们的斜率之积等于 -1（或它们的斜率是负倒数）。

垂直公理

给定一条直线，${\overleftrightarrow {AB}}$，以及不在直线 ${\overleftrightarrow {AB}}$ 上的点 P，则只有一条直线通过点 P 且垂直于 ${\overleftrightarrow {AB}}$

平面

当且仅当一个物体是二维的、没有厚度或曲率并无限延伸时，它才是平面。平面可以用三个点来定义。平面可以被认为类似于一张纸[1]。

点

点是一个零维的数学对象，代表一个或多个维度中的位置[2]。点没有大小；它只有位置。

多边形

多边形是由至少 3 条直线组成的封闭平面图形。每条边都必须在其各自的端点处与另一条边相交，并且相交的线不是共线的。

R

半径

圆的半径是圆上任意一点到圆心的距离。

同一个圆（或全等圆）的所有半径具有相同的度量。

参见 圆

射线

射线是一个直线点集，它在一个方向上无限延伸。射线停止的点被称为射线的端点。在射线上的任意两点之间，存在无限多个也包含在射线中的点。

正多边形

正多边形是等边且等角的多边形。

尺规公理

直线上的点可以与实数一一对应。对应于点的实数是该点的坐标。两点之间的距离是两点坐标之差的绝对值。

S

半圆

弧度为 180 度的弧。

多边形内角和

具有 n 个边的多边形的内角和的计算方法为

内角和 = (n-2)180

补角

当且仅当两个角的度数之和等于 180 度时，这两个角互为补角。

导航

• 几何学主页
• Motivation
• Introduction
• Geometry/Chapter 1 - HS 定义和推理（介绍）
  • Geometry/Chapter 1/Lesson 1 简介
  • Geometry/Chapter 1/Lesson 2 推理
  • 几何/第 1 章/第 3 课 未定义术语
  • 几何/第 1 章/第 4 课 公理/公设
  • 几何/第 1 章/第 5 课 定理
  • 几何/第 1 章/词汇 词汇
• 几何/第 2 章 证明
• 几何/第 3 章 逻辑论证
• 几何/第 4 章 全等和相似
• 几何/第 5 章 三角形：全等和相似
• 几何/第 6 章 三角形：不等式定理
• 几何/第 7 章 平行线、四边形和圆
• 几何/第 8 章 周长、面积、体积
• 几何/第 9 章 棱柱、棱锥、球体
• 几何/第 10 章 多边形
• 几何/第 11 章 $\mathbb {R} ,\mathbb {R} ^{2},\mathbb {R} ^{3}$
• 几何/第 12 章 角：内角和外角
• 几何/第 13 章 角：余角、补角、对顶角
• 几何/第 14 章 勾股定理：证明
• 几何/第 15 章 勾股定理：距离和三角形
• 几何/第 16 章 作图
• 几何/第 17 章 坐标几何
• 几何/第 18 章 三角学
• 几何/第 19 章 三角学：解三角形
• 几何/第 20 章 特殊直角三角形
• 几何/第 21 章 弦、割线、切线、圆内角、圆外角
• 几何/第 22 章 刚性运动
• 几何/附录 A 公式
• 几何/附录 B 问题答案
• 附录 C. 几何/公理与定义
• 附录 D. 几何/SMSG 欧氏几何公理