几何/第 7 章
在欧几里得几何中,如果两条直线不相交,则它们是平行的。
请记住,直线无限延伸,如果它们不平行,它们最终会相交。
画一条直线 AB,画一条平行于 AB 的直线 CD
找到一种方法来证明 AB 平行于 CD
在欧几里得几何中,如果两条直线相交成 90 度角,则它们是垂直的。

画一条直线 AB,然后在直线 AB 上选取一个点 C,画一条与 C 相交且垂直于 AB 的直线,即
证明直线 CD 垂直于 AB。
全等圆形是指大小相同,即半径相同的圆形。
同心圆形共享相同的中心、轴或原点,一个在另一个里面。同心圆形不一定具有相同的半径。
画一个圆形,找到一种方法来画一个全等圆形,证明它们是全等的
画一个圆形,然后画一个同心圆形,证明它们是同心圆形。
半径是连接圆形上一点和圆心的一条线段。
直径是连接圆形上两点并穿过圆心的线段。
弦是连接圆形上两点的线段,它不必穿过圆心。圆形的直径是最长的弦。
四边形被定义为任何四边多边形。这意味着正方形、矩形等都被称为四边形。在以下章节中,我们将仔细研究每个重要的四边形,它们是如何定义的,以及它们各自的一些特殊属性。
矩形被定义为具有 4 个条件。第一个是它是一个四边多边形。第二个是它有两对平行边。第三个是平行边对的长度相等。第四个是所有角必须等于 90 度或直角。
让我们举个例子。下面是一个矩形。首先我们注意到它有 4 条边,它们形成一个多边形,这使得它成为一个四边多边形,因此满足了第一个条件。接下来我们注意到 2 条边彼此平行,另外 2 条边也彼此平行,因此满足了第二个条件。现在我们注意到平行边对的长度相等,因此满足了第三个条件。最后一个条件是所有角必须是 90 度,如图像所示,它们实际上是 90 度。因为所有 4 个条件都已满足,我们现在知道下面的多边形实际上是一个矩形。
好的,现在矩形已经定义好了,我们需要知道矩形有什么特别之处。
对角线的长度
下面是与上面相同的矩形,只是它有一条从一个顶点到另一个顶点的对角线。这条对角线的长度等于一边平方加上相邻边平方之和的平方根。例如:
这个证明非常简单。但是首先你必须知道勾股定理,如果你还没有了解它,请先阅读一下。
1) ∠ABC = 90 度 - 矩形的定义所给。
2) AB 边和 BC 边以及对角线构成一个三角形。- 一个三边形。
3) 这个三角形也是一个直角三角形,因为它有一个直角。- ∠ABC
4) 矩形的对角线是三角形的斜边。
5) 直角三角形的斜边等于两条直角边的平方和的平方根 - 勾股定理
6) 因此,对角线等于
根据此特性,我们可以注意到,如果我们画一条对角线,就会在矩形内创建两个全等的三角形。
证明
下面是一个画了对角线的矩形。我们把顶点命名为 A、B、C、D。对角线称为 AC,因为两个端点是 A 和 C。两个三角形是 ABC 和 ADC。

1) 两个三角形共用一条边 - AC。
2) AD 和 BC 的长度相等 - 已知。
3) ∠ABC 和 ∠ADC 的度数相等 - 矩形的定义。
4) 每个三角形都有一个度数相等的角 - 语句 3。
5) 根据边角边定理,每个三角形都是全等的。
例子
[edit | edit source]正方形
[edit | edit source]正方形具有与矩形相同的性质,只是所有 4 条边必须长度相等。正方形也被认为是菱形、风筝形、平行四边形和梯形。
特殊属性
[edit | edit source]例子
[edit | edit source]梯形
[edit | edit source]梯形是四边形,其中两条边平行。

特殊属性
[edit | edit source]梯形的面积由以下公式给出:
,其中 a 和 b 是两条平行边的长度,h 是高度。
例子
[edit | edit source]<1=
菱形
[edit | edit source]菱形是四边形,四边相等。

特殊属性
[edit | edit source]菱形的面积由以下公式给出:
其中 D1 和 D2 是两条对角线的长度
因为菱形是平行四边形,所以面积也等于一条边的长度 (B) 乘以两条相对边之间的垂直距离 (H)
面积也等于边长的平方乘以任何一个内角的正弦
其中 a 是边的长度, 是两条边之间的角度。
例子
[edit | edit source]平行四边形
[edit | edit source]平行四边形是四边形,有两组平行边。
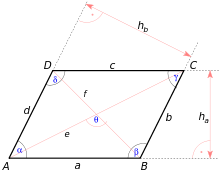
特殊属性
[edit | edit source]平行四边形的面积
- 其中 B 是底,H 是高
平行四边形的对角线互相平分。
例子
[edit | edit source]导航
- 几何学主页
- 动机
- 介绍
- 几何学/第 1 章 - 高中 定义和推理(引言)
- 几何学/第 1 章/第 1 课 介绍
- 几何学/第 1 章/第 2 课 推理
- 几何学/第 1 章/第 3 课 未定义术语
- 几何学/第 1 章/第 4 课 公理/公设
- 几何学/第 1 章/第 5 课 定理
- 几何学/第 1 章/词汇 词汇
- 几何学/第 2 章 证明
- 几何学/第 3 章 逻辑论证
- 几何学/第 4 章 全等和相似
- 几何学/第 5 章 三角形:全等和相似
- 几何学/第 6 章 三角形:不等式定理
- 几何学/第 7 章 平行线、四边形和圆
- 几何学/第 8 章 周长、面积、体积
- 几何学/第 9 章 棱柱、棱锥、球体
- 几何学/第 10 章 多边形
- 几何/第 11 章
- 几何/第 12 章 角:内角和外角
- 几何/第 13 章 角:余角、补角、对顶角
- 几何/第 14 章 勾股定理:证明
- 几何/第 15 章 勾股定理:距离和三角形
- 几何/第 16 章 作图
- 几何/第 17 章 坐标几何
- 几何/第 18 章 三角学
- 几何/第 19 章 三角学:解三角形
- 几何/第 20 章 特殊直角三角形
- 几何/第 21 章 弦、割线、切线、圆内角、圆外角
- 几何/第 22 章 刚性运动
- 几何/附录 A 公式
- 几何/附录 B 答案
- 附录 C. 几何/公理与定义
- 附录 D. 几何/SMSG 欧几里得几何公理
















