几何/附录 C

A

锐角

参见 角

等式代数性质

对于实数 a、b 和 c

加法等式性质：如果 a=b，则 a+c=b+c

减法等式性质：如果 a=b，则 a-c=b-c

乘法等式性质：如果 a=b，则 ac=bc

除法等式性质：如果 a=b 且 c≠0，则 (a/c)=(b/c)

对称等式性质：如果 a=b，则 b=a

传递等式性质：如果 a=b 且 b=c，则 a=c

自反等式性质：如果 a=a，则 a=a

替换等式性质：如果 a=b，则 a 可以用 b 代替

分配等式性质：a(b+c)=ab+ac

角

角 ABC 是锐角。

当且仅当一个图形由两条共享一个公共端点的射线组成时，该图形为一个角。每条射线（或线段，视情况而定）被称为该角的边（例如，${\overline {AB}}\;$ 在右边的插图中），公共点被称为角的顶点（在插图中为点B）。角的测量是通过其斜率之差来衡量的。角的测量单位是弧度和度数。角可以根据其度数进行分类。

• 锐角：当且仅当一个角的度数小于 90° 时，该角为一个锐角
• 直角：当且仅当一个角的度数恰好为 90° 时，该角为一个直角
• 钝角：当且仅当一个角的度数大于 90° 时，该角为一个钝角
• 平角：当且仅当一个角的度数恰好为 180° 时，该角为一个平角

根据直角全等定理和平角全等定理，所有直角和所有平角都全等

角加法公理

如果 P 在角 $\angle ABC$ 的内部，则 $\angle ABC=\angle ABP+\angle PBC$

算术平均值

2 个数字 a 和 b 的算术平均值可以计算为：算术平均值 = (a+b)/2

B

角平分线

当且仅当一个图形将它所相交的图形分成两个相等的部分时，该图形平分另一个图形

C

圆心

点P 是圆C 的圆心，当且仅当圆C 中的所有点都与点P 等距，并且点P 与圆C 在同一个平面内。

圆

平面中与一个给定点（称为圆心）等距的所有点的集合。

圆周

圆的周长。

计算公式为

C=2πr（其中r为圆的半径）

余角

如果且仅当两个角的度数之和等于90度，则这两个角互为余角。

凹

如果且仅当一个多边形至少包含一个内角，其度数大于180°且小于360°，则该多边形被称为凹多边形。

全等

如果且仅当两个图形具有相同的度量，则这两个图形全等。用"≅"表示。

对应角

有四对对应角: ∠1 和 ∠3，∠2 和 ∠4，∠5 和 ∠7，以及 ∠6 和 ∠8。

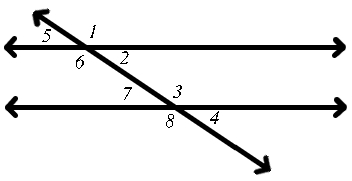
如果且仅当一条横截线与两条直线相交形成的两个角，一个位于两条直线内部，另一个位于两条直线外部，且都在横截线的同一侧，则这两个角互为对应角。

对应角定理

如果两条直线被一条横截线所截，则它们之间的对应角相等。

全等三角形的对应边和对应角相等定理

全等三角形的对应边和对应角相等定理 (CPCTC) 表明

如果 ∆ABC ≅ ∆XYZ，那么 ∆ABC 的所有部分都与其在 ∆XYZ 中的对应部分相等。例如

• ${\overline {AB}}\;$ ≅ ${\overline {XY}}\;$

• ${\overline {BC}}\;$ ≅ ${\overline {YZ}}\;$

• ${\overline {AC}}\;$ ≅ ${\overline {XZ}}\;$

• ∠ABC ≅ ∠XYZ

• ∠BCA ≅ ∠YZX

• ∠CAB ≅ ∠ZXY

CPCTC 也适用于三角形的所有其他部分，如三角形的高、中线、外心等。

余弦

一个三角函数，缩写为 cos。

cos(θ)=邻边/斜边

D

直径

如果且仅当一条线段是圆的弦并且包含圆心，则该线段是圆的直径。

参见 圆

距离

两点之间的距离可以计算为这两点坐标差的绝对值。

在坐标系中，点 A(x₁,y₁) 和 B(x₂,y₂) 之间的距离可以计算为

d(AB)=√((y₂-y₁)²+(x₂-x₁)²)

点和直线之间的距离由连接这两者的垂直线段测量（使用垂直定理）。

G

几何平均数

对于两个正数 a 和 b，a 和 b 的几何平均数是满足 (a/x)=(x/b) 的正数 x。因此，x²=√(ab)

a 和 b 的几何平均数 = (a/x)=(x/b) : x²=√(ab)

H

平行四边形的高度

平行四边形两底之间的垂直距离

斜边

在直角三角形中，直角所对的边。

使用勾股定理，斜边的度量可以计算为

c²=a²=b²（其中 c 为斜边，a 和 b 为直角三角形的两条直角边）

L

线

点集为直线当且仅当点集完全直线（对齐），无限长，无限薄。 在直线上的任意两点之间，存在无限数量的点也包含在直线中。 直线通常用直线上的两点表示，例如直线AB，或 ${\overleftrightarrow {AB}}$

线段

线段MN

点集为线段当且仅当它完全直线，无限薄，且具有有限长度。 线段的度量由线段上两个极端点（称为端点）之间的最短距离测量。 在线段上的任意两点之间，存在无限数量的点也包含在线段中。

我

正多边形的内角

正多边形的内角都全等。 因此，可以计算出具有n个边的正多边形的一个内角的度数

int angle = ((n-2)180)/n

等腰梯形

腰长相等的梯形。

等腰三角形

至少有两条边相等的三角形。

利用底角定理，与全等边相对的角也全等。

L

线性对

非公共边为相反射线的相邻角。

利用线性对定理，线性对中的角也互补。

如果构成线性对的两个角全等，则这两个角都是直角，且包含这两个角的直线垂直。

M

优弧

度数大于 180 度的弧。 它必须用 3 个点命名。

梯形的中位线

连接梯形腰中点的线段。

它平行于底，其长度是底长度算术平均值。

劣弧

度数小于 180 度的弧。

P

平行线

两条直线或线段被称为平行，当且仅当这些直线包含在同一个平面中，并且如果无限延伸，则它们没有公共点。

在坐标平面上，两条直线平行当且仅当它们具有相同的斜率。

平行平面

两条平面被称为平行，当且仅当这些平面无限延伸时没有公共点。

垂直线

在 90° 角处相交的两条直线。

在坐标平面上，两条直线垂直当且仅当它们的斜率的乘积等于 -1（或者如果它们的斜率是负倒数）。

垂直定理

给定一条直线，${\overleftrightarrow {AB}}$ 和一个不在直线 ${\overleftrightarrow {AB}}$ 上的点 P，那么只有一条直线经过点 P 垂直于 ${\overleftrightarrow {AB}}$

平面

物体为平面当且仅当它是二维物体，没有厚度或曲率，并且无限延伸。 平面可以用三个点定义。 平面可以被认为类似于一张纸[1].

点

点是一个零维的数学对象，代表着一个或多个维度中的位置[2]。点没有大小，只有位置。

多边形

多边形是一个封闭的平面图形，由至少 3 条直线组成。每条边必须在其各自的端点处与另一条边相交，并且相交的直线不共线。

R

半径

圆的半径是圆上任意一点到圆心的距离。

同一个圆（或全等圆）中所有的半径长度都相同。

参见 圆

射线

射线是由一系列直线点组成的，这些点在一个方向上无限延伸。射线停止的点被称为射线的端点。在射线上的任意两个点之间，存在无限多个也包含在射线中的点。

正多边形

正多边形是等边且等角的多边形。

尺规作图公理

直线上的点可以与实数一一对应。对应于点的实数是点的坐标。两点之间的距离是这两点坐标之差的绝对值。

S

半圆

度数为 180 度的弧。

多边形的内角和

一个有 n 条边的多边形的内角和的计算公式为：

内角和 = (n-2)180

互补角

当且仅当两个角的度数之和等于 180 度时，这两个角互补。

导航

• 几何学主页
• 动机
• 简介
• 几何学/第一章 - 高中 定义和推理（简介）
  • 几何学/第一章/第一节 简介
  • 几何学/第一章/第二节 推理
  • 几何学/第一章/第三节 未定义术语
  • 几何学/第一章/第四节 公理/公设
  • 几何学/第一章/第五节 定理
  • 几何学/第一章/词汇表 词汇表
• 几何学/第二章 证明
• 几何学/第三章 逻辑论证
• 几何学/第四章 全等和相似
• Geometry/Chapter 5 三角形：全等与相似
• Geometry/Chapter 6 三角形：不等式定理
• Geometry/Chapter 7 平行线、四边形和圆形
• Geometry/Chapter 8 周长、面积、体积
• Geometry/Chapter 9 棱柱、棱锥、球体
• Geometry/Chapter 10 多边形
• Geometry/Chapter 11 $\mathbb {R} ,\mathbb {R} ^{2},\mathbb {R} ^{3}$
• Geometry/Chapter 12 角：内角和外角
• Geometry/Chapter 13 角：余角、补角、对顶角
• Geometry/Chapter 14 勾股定理：证明
• Geometry/Chapter 15 勾股定理：距离和三角形
• Geometry/Chapter 16 作图
• Geometry/Chapter 17 解析几何
• Geometry/Chapter 18 三角函数
• Geometry/Chapter 19 三角函数：解三角形
• Geometry/Chapter 20 特殊直角三角形
• Geometry/Chapter 21 弦、割线、切线、圆周角、外角
• Geometry/Chapter 22 刚性运动
• Geometry/Appendix A 公式
• 几何/附录 B 习题答案
• 附录 C. 几何/公理和定义
• 附录 D. 几何/SMSG 欧几里得几何公理